Hur man beräknar avståndet till horisonten

1. 1
   Mät din "ögonhöjd." Mät längden mellan marken och din i meter eller fot. Ett sätt att beräkna detta är att mäta avståndet mellan din och toppen av huvudet. Subtrahera detta värde från din totala höjden och vad blir kvar är avståndet mellan ögonen och ytan du står på. Om du står precis vid havet, med botten av din fot nivå med vattnet, är detta den enda mätning du behöver.
2. 2
   Lägg till din "lokala höjd" om du står på en upphöjd yta, t.ex. ett berg, byggnad eller båt. Hur många meter eller fot ovanför den verkliga horisonten står ni? 1 meter? 4000 meter? Lägg till att numret till din ögonhöjd (i samma enheter, förstås).
3. 3
   Multiplicera med 13m om du tog mätningen i meter, eller multiplicera med 1.5ft om du tog mätningen i fötterna.
4. 4
   Ta kvadratroten för att hitta svaret. Om du använde meter, kommer svaret att vara i kilometer, och om fötterna, kommer svaret att vara i miles. Avståndet beräknas är en rak linje från dina ögon till horisonten. Den faktiska avståndet du resa för att komma till horisonten blir längre på grund av ytkrökning och (på land) oegentligheter. Fortsätt till nästa metod nedan för en mer korrekt (och komplicerade) formel.
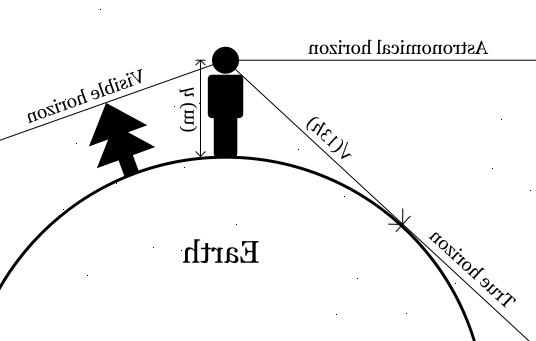
5. 5
   Förstå hur denna beräkning fungerar. Den är baserad på en triangel som bildas av din observation punkt (ögonen), den sanna horisonten punkten (vad du tittar på) och centrum av jorden. Genom att veta radien av jorden och mäta din ögonhöjd och lokal höjd, lämnar det bara avståndet mellan dina ögon och horisonten som okänd. Eftersom sidorna av triangeln som möts vid horisonten faktiskt bildar en rät vinkel, kan vi använda Pythagoras sats (gamla goda a ^ 2 + b ^ 2 = c ^ 2) som grund för denna beräkning, där:
   • a = R (radien av jorden)
   • b = avståndet till horisonten, okända
   • c = h (din ögonhöjd) + R

Alternativ metod # 1

1. 1
   Beräkna det faktiska avståndet du måste korsa för att komma till horisonten med hjälp av denna formel:
   d = R * arccos (R / (R + h))
   d = avståndet till horisonten
   h = ögonhöjd
   
2. 2
   Öka R med 20% för att kompensera för den snedvridande brytning av ljusstrålar och att komma fram till en mer exakt mätning. Den geometriska horisonten beräknas enligt denna artikel får inte vara samma som den optiska horisonten, vilket är vad ögat faktiskt ser. Atmosfären böjar (bryter) ljus som färdas horisontellt. Vad detta betyder oftast att en ljusstråle kan lätt följa krökningen av jorden, så att den optiska horisonten är lite längre bort än den geometriska horisonten. Tyvärr refraktion grund av att atmosfären är varken konstant eller förutsägbar, eftersom det beror på förändringen av temperaturen med höjden. Det finns alltså inget enkelt sätt att lägga till en korrigering av formeln för den geometriska horisonten, även om man kan uppnå en "genomsnittlig" genom att anta en radie på jorden som är lite större än den verkliga radien.
3. 3
   Räkna ut hur denna beräkning fungerar. Detta kommer att beräkna längden på den kurva som följer från dina fötter till den verkliga horisonten (visas i grönt på bilden). Nu hänvisar arccos (R / (R + h)) portion till den vinkel som görs i mitten av jorden med linjen som går från den sanna horisonten till centrum och linjen går från dig till centrum. Med denna vinkel, multiplicerar vi det med R för att få den "båglängd," som, i det här fallet, är det avstånd som du letar efter.
   

Alternativ metod # 2

1. 1
   Antag en platt plan eller havet. Denna metod är en enklare version av den första uppsättningen av instruktioner som presenteras i den här artikeln, och gäller endast i fot och miles.
2. 2
   Lös för avståndet i miles genom att koppla in din ögonhöjd i fot (h) i följande formel:
   d = 1,2246 * ROT (h)
   
3. 3
   Härled formeln från Pythagoras sats.
   (R + h) ^ 2 = R ^ 2 + d ^ 2
   Lösa för h (. Göra antagandet att R >> h och uttryck av jordradien i miles, ca 3959) ger uttrycket:
   d = ROT (2 * R * h)